INTRODUCTION
The centrepiece of this post comes courtesy of the team4nature twitter account. I have also included the solution to a prnblem from brilliant.org and a new problem from the same source.
WALK FOR WILDLIFE

A SOLUTION AND A NEW PROBLEM
Here is the answer the problem I posed last week:
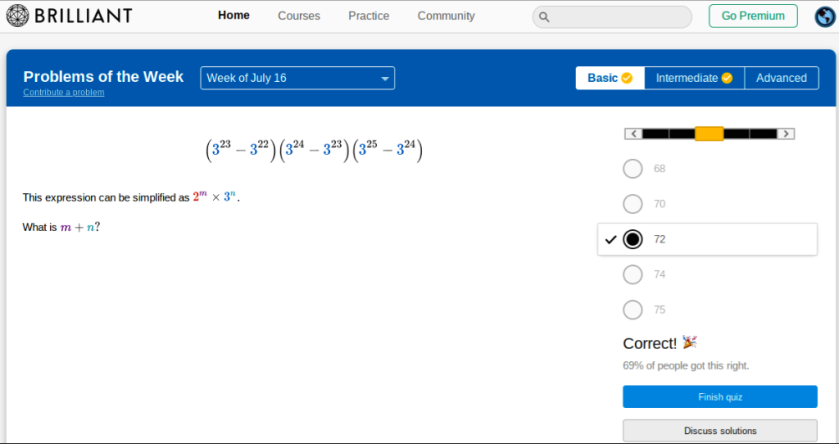
carrying out the subtractions in thte brackets above gives us (2 * 3^22)(2 * 3 ^23)(2 * 3^24). This becomes (2^3)(3^(22+23+24))= (2^3)(3^69). Thus m = 3 and n = 69, and 69 + 3 = 72.
As a supplement to this little problem, would you have an observation platform where the three bridge segments meet at the centre of the lake? This latter of course, unlike the mathematical question is purely a matter of opinion. I would go for a circular platform just below the level of the bridges, accessible by lifts and stairs.


