INTRODUCTION
A couple of days ago I set some puzzles for you, and in this post I will be answering them. Also, I am off to Greece for a week’s holiday later tonight (I fly out of Gatwick at 5:40AM, so am envisaging taking the 21:36 train out of Lynn, connecting to a Thameslink service at St Pancras and arriving the airport just after 1AM – the second latest set of connections available to me, and I know British public transport too well and trust it too little to rely on the last possible connections) and although I will take any opportunities that arise to go online I will still have comparatively little access to the internet, so you will hear little from me between now and a week tomorrow evening when I shall be back home.
SOLUTION 1: DR FRANKENINE

Here is the most elegant of the official solutions, posted by Callum Cassidy-Nolan:

SOLUTION TWO: FUEL TANK
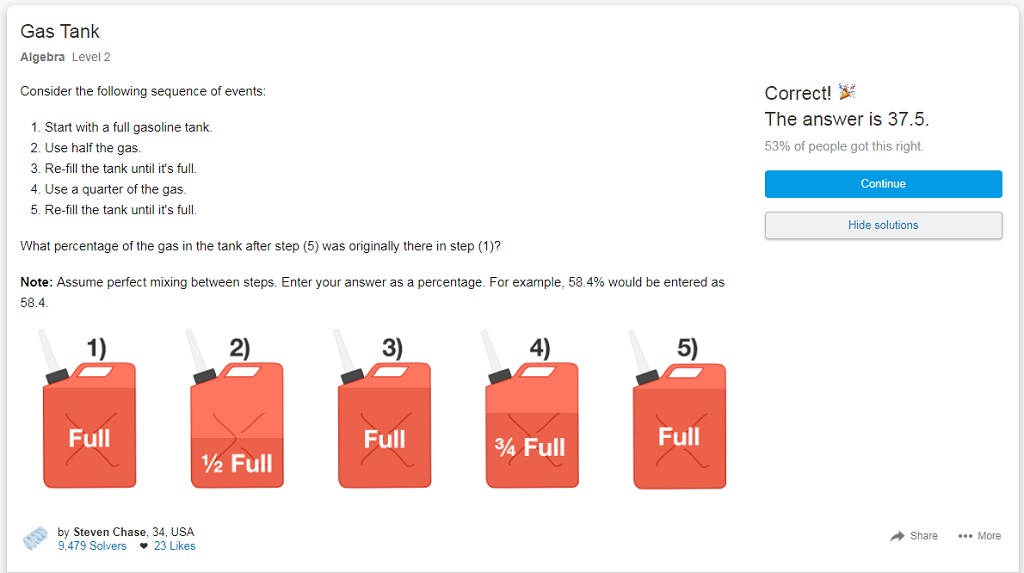
As you can see from the above graphic, almost half of those who attempted solutions on brilliant.org got it wrong. A perusal of the comments section revealed a degree of reluctance on the part of some of the errant solvers to admit to being wrong (never mind arguing with the umpire, some of these folk were metaphorically following that up by arguing with TV replay umpire) so I am to explain the whole process of getting the right answer (though it took me milliseconds to work out and not much longer to enter the correct answer):
- After stage 2) half of the original fuel remains and is then topped up with new fuel, and we are told to assume that perfect mixing occurs…
- After stage four one quarter of the tank of perfectly mixed fuel has gone, and as it is perfectly mixed one half of that fuel is original, meaning that a further one eighth of total tank full of original fuel has been used.
- One half plus one eighth = five eighths of the original tank full of fuel has been used, leaving three eighths of the original tank full still there.
- As a percentage three eighths is 300/8 = 37.5 per cent, and the question has asked for that figure.
One particularly offensive complainant attempted to use the fact that the question had said decimals allowed to claim that an answer of 0.375 should have been permitted. This is wrong – the question specifically asked for a percentage, and the reason for mentioning the a decimal figure was OK was so that people did not think they needed to round to the nearest whole number, which in correct mathematical notation would have been 38 (the figure being rounded away is five or greater so you round up, had it been four or less it would have been correct to round down).
Another complaint people made was being marked wrong for including the percentage symbol – I am less unsympathetic to this than I am to the indefensible claim that 0.375 should have been marked as right, as this latter has missed out turning the answer into a percentage, but including the symbol is still a mistake as the way the question is asked renders it needless to do so.
Please note that I did not create this problem and had nothing to do with deciding what answer should be marked as right – I have treated it at length because I was annoyed on the composers behalf that so many solvers rather than attempting to see by looking at correct solutions, of which plenty of good ones were posted, why their chosen answer was wrong instead opted for the ‘argue with the umpire’ approach, in some cases being very unpleasant about it. Here to end this little post is David Vreken’s published solution: