Tag: Mathematics

Answer to the Pythagorean Problem

The answer to a problem incliuded in yesterday’s post Monday Miscellany.

INTRODUCTION

You may remember that in yesterday’s post titled “Monday Miscellany” I included one of the problems I had solvced on the mathematical website Brilliant – this post presents the solution and also clears up a side issue raised on that website by disgruntled folk who had got it wrong.

THE PROBLEM

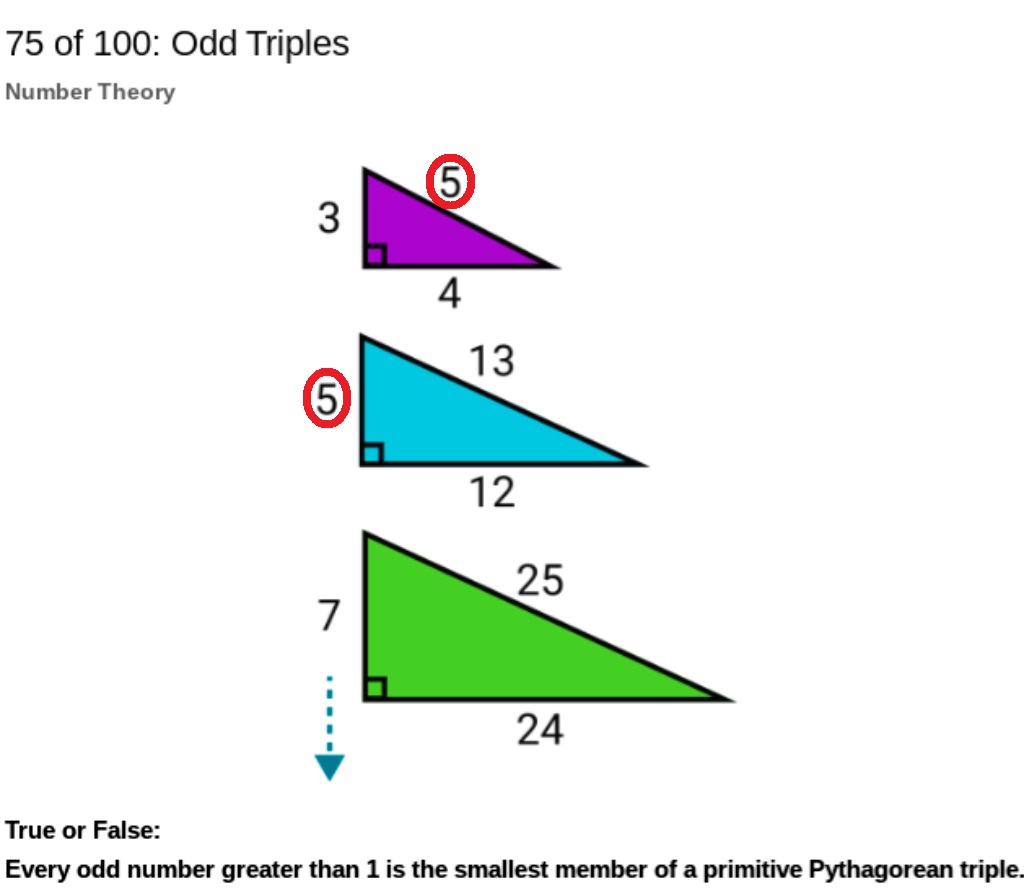
Here is the problem again from yesterday:

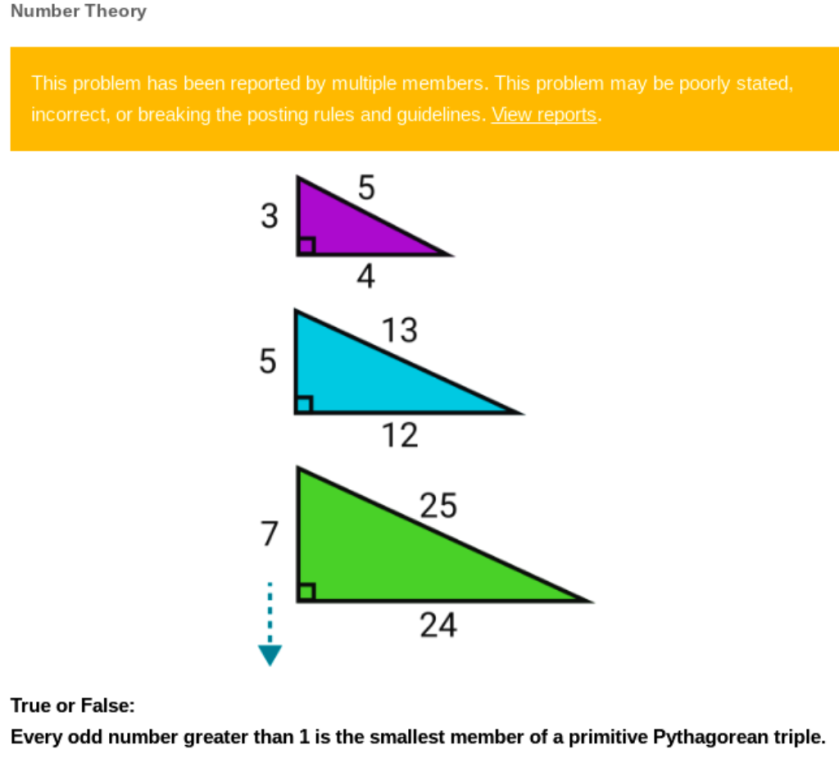
Pythag

THE SOLUTION

The answer is True. The formula for (x+1)^2 is X^2 + 2X + 1, and every odd number greater than 1 could serve as the 2X+1 part of that equation. 

THE SIDE ISSUE

Some people on Brilliant cavilled at this because there are some Primitive Pythagorean Triples whose smallest term is even (8,15, 17, 20,21,29 and 65,72,97 were all mentioned, although none of the complainers mentioned 12,35,37, 60,91,109 or 696,697,985). The question did not state that the triple of which the odd number is the lowest term was the lowest triple to feature that number, and indeed if one looks carefully at the triangles presented as part of the problem one can see clearly that the odd number is allowed to be in another triple where it is not the lowest term:

Pythagorean Triples Solution - a

Note that the number 5 features twice (ringed in the diagram above, once as the largest term in a triple and once as the smallest).

Thus that 15 features in 8,15,17 does not invalidate the claim of the question since it is the smallest term in 15, 112, 113. All the other odd numbers mentioned in triples of which they are not the smallest member likewise feature in triples in which they are the smallest member, the biggest being 985, 485112, 485113. 

Monday Miscellany

A mixed bag of an offering this Monday afternoon!

INTRODUCTION

This post will be every bit as varied as its title suggests, featuring a mix of politics, mathematics, music, nature and photography (and possibly more). 

SOME MATHS RELATED STUFF

I start with one of more recent followers, RobertLovesPi, and I have several pieces of his to share:

My next piece, courtesy of whyevolutionistrue is titled “The Coffer Illusion“, which concerns the picture below:

If the illusion defeats you, you can find out where the circles are by going to the original post. 

I finish this little section with a nod to the mathematical website Brilliant, which I am a regular visitor to (I am currently on a 64 day problem solving streak). As a sample here is a problem I solved today, rated at maximum difficulty by the site, pretty close to minimum by me:

Pythag

You can look at solutions to this problem on the website, and I will reveal the answer on this blog tomorrow. 

A FEW POLITICAL PIECES

There has been a lot of coverage from various people of events in Charlottesville. I choose to draw your attention to Richard Murphy’s excellent piece on Tax Research UK, titled “Charlottesville is a cradle of extremism: we should take note“. Below is a screenshot of the first few paragraphs:

charlottesville

My second link is to the petitionsite, regarding a young women in El Salvador who having been raped and then had a miscarriage has then been jailed for 30 years due to the Catholic church influence anti-abortion laws of that country. The screenshot below is formatted as a link to take you to this petition to sign and if possible share it:

Screenshot 2017-08-14 at 3.29.29 PM

I finish this section on a lighter note, courtesy of whyevolutionistrue. This little piece titled “Where is North Korea? Some Americans have no idea” reminds us how unacquainted USians are with that area known as the rest of the world! Here is a screenshot of the opening paragraph:
Screenshot 2017-08-14 at 3.39.40 PM

PHOTOGRAPHS

I usually end my blog posts with some of my own photographs, but this photograph section has an additional feature – as a nod to the principal subjects of many of the photos that follow I offer you a musica prelude – Ottorino Respighi’s “The Birds”:

cormorants and boatCormorants8Cormorant headsCormorants6Cormorants4Cormorants3Cormorants2Cormorants1Cormorants and gull 5Cormorant4Cormorants11Cormorants 10Cormorants and gull3TerngullCormorant3Cormorant2

Cormorant
I did not notice the white bird on the far side of the river until I was editing this one – I think from the shape and colour that is a Little Egret but the image is not clear enough to be sure.

Cormorants and swimming gullPollinator3Flybutterfly wingPollinator2white butterflyPollinator

Squirrel does Meerkat impression
This squirrel is clearly an impressionist – and his meerkat is very good!

An Important Petition and a Puzzle

A link to an excellent and important petition, and also a mathematical teaser.

INTRODUCTION

There will be no photographs in this post, but I wanted to put something up today because I several new people are following this blog – my thanks to you all.

THE PUZZLE

This puzzle comes from one my books at home (cannot remember which) and has a particular relevance which I will reveal in my next post: take any three digit number, and multiply by 7, then multiply the new number 11 and finally multiply that number by 13. What do you notice about this latest answer as compared to your original number? For a bonus what two numbers would you need to use as multipliers to achieve an equivalent effect with a four digit starting number?

A REALLY EXCELLENT PETITION

My latest twitter follower, Laura Warwick by name, has created a petition on the British government’s official petitions site (which means it is open only to UK citizens to sign) calling on the government to not allow train companies to increase their fares until they have improved their services. Click the screenshot below to sign and share the perition:

petition

Congratulations to England Women’s XI

INTRODUCTION

While Alastair Cook and his team are fighting hard in Visakhapatnam, the women have recorded a tremendous victory in Colombo.

A SPECTACULAR RECOVERY

You may recall that in my last post I detailed the recovery of the England Women’s innings from 58-6 20 241-9 in their 50 overs. Rain then intervened, so the players reconvened today for the Sri Lankan response. Natalie Sciver, whose 77 dug England out of trouble followed up by accounting for both Sri Lankan openers. Danielle Hazell and Laura Marsh who had continued to Sciver inspired batting recovery then cashed in on the early breakthroughs , Marsh taking 4-21 from her full ten overs and Hazell finishing with 3-21 from 8.1 overs.

While all three of the young women mentioned above performed outstandingly I would say that Sciver who played the major innings and then made the early breakthroughs that the other two capitalised on was the key to this astonishing turnaround. The cricinfo scorecard makes no mention of a Player of the Match award, but if there was one it should have gone to Sciver with honourable mentions for Hazell and Marsh.

THE SOLUTION TO THE MATHS TEASER

Below is the pair of simultaneous equations from my last post – the challenge was to pick and solve one of these pairs:

73X + 43y = 211                     685,463X + 314,537Y = 2,685,463
31x + 83y = 199                     314,537X + 685,463Y = 2,314,537

If you did the non-mathematicians thing of selecting the pair of equations featuring smaller numbers you get zero credit. If however you managed to avoid being scared by the large numbers in the second pair you might have noticed that the number of Xs in the first pair equals the number of Ys in the second and vice versa, or in other words, temporarily removing the numbers we have:

aX + bY = c
bX + aY = d

This gives us options for possibly simplifying the equations. First up let us look at adding the two initial equations together which gives us:

(a+b)X + (a+b)Y = c+d

Feeding the numbers back in, we get:

1,000,000X + 1,000,000Y = 5,000,000 which simplifies nicely to X + Y = 5

we can also subtract the bottom equation from the top one, giving us:

aX – bY = c-d

Feeding the numbers back in gives us 370,926X – 370,926Y = 370,926, which at first glance may not look terribly pleasant, but a second glance shows that the number of Xs and Ys are equal and that that number appears on the other side of the new equation, so in other words it simplifies to X – Y = 1.

Thus the solution to the original pair of equations with those huge numbers is the solution to this pair of equations:

X + Y = 5
X – Y = 1

Thus X = 3 and Y = 2.

SOME PICTURES TO FINISH

234-a
These images are all of lots in our December auction (takes place on the 14th), starting with some coins

234-b242-a242-b243-a243-b244-a244-b245-a245-b

556
Lot 556 (4 images)

556-a556-b556-c

557
Lot 557 (2 images)

557-a

593
Lot 593, four images. This is a particularly fine specimen of the Kukri or Khukuri, the knife carried by Gurkha warriors.

593-a593-b593-c

 

 

Forty

INTRODUCTION

This is a different post from my usual style – there will be no pictures, and just the one link which I feel must be shared and which will feature at the end of the post.

FORTY

It is inevitable when writing about the number 40 that there will be considerable overlap with the detail contained in Derrick Niedermann’s wonderful book Number Freak but I hope that some of the stuff I come with is new. One of the things Niedermann talks about is the use of forty in ancient times to denote ‘a large number’ in which he context he mentions various biblical references and the tale of Ali Baba and the Forty Thieves – which reference particularly appeals as I am the proud owner of both a four volume boxed set of the complete 1,001 nights and a Folio Society edition of the highlights.

SOME OF THE PROPERTIES OF THE NUMBER 40

It can be expressed as the sum of a square and a triangle in two different ways: Two squared added to the eighth triangle number or five squared added to the fifth triangle number (note 8+2 = 10 and 5+5 = 10).

It is both double and quadruple a tetrahedral number (10= 1+3+6 = the sum of the first three triangle numbers and 20 + 1+3+6+10 = the sum of the first four triangle numbers).

It is the sum of the fourth triangle and the fourth pyramid number (10 = 1+2=3+4 and 30 = 1+4+9+16) and it is also thus the sum of third tetrahedral number and the fourth pyramid number.

Another connection of two fours and forty is that four squared plus 4 factorial = 16 + 24 = 40.

WHY THE NUMBER 40?

I have written about the number 40 because today is my 40th birthday and I thought this would be a fun way to commemorate the landmark for followers of my blog.

THAT ONE LINK

I am sharing one link with this post, from Autsim Mom, who will be visiting this country shortly. This post was first published before I had started following that blog and I am delighted to share it now.