Solutions to Good and Bad Mathematical Problems

Solutions to the problems I put up here on saturday and some new problems.

INTRODUCTION

On Saturday I produced a mixed bag of offerings from brilliant.org, promising to provide solutions in a later post, and now that time has arrived.

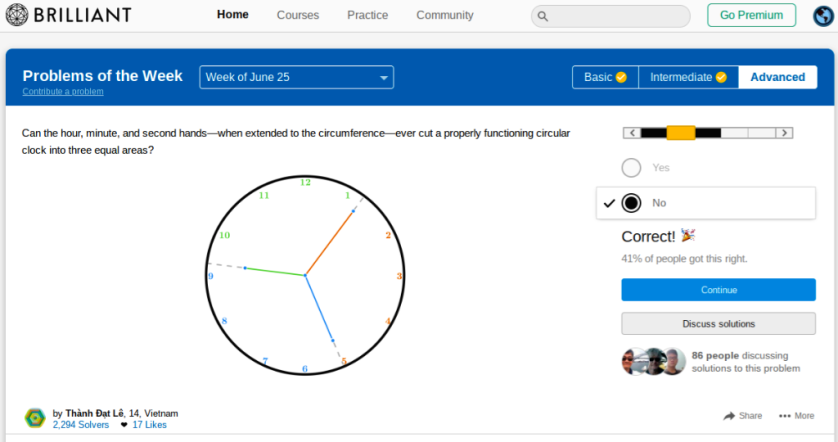
THE WORST SET PROBLEM I HAVE EVER ENCOUNTERED ON BRILLIANT

I got nowhere close to solving this for reasons which will soon become obvious.

Here is the official “correct” answer:

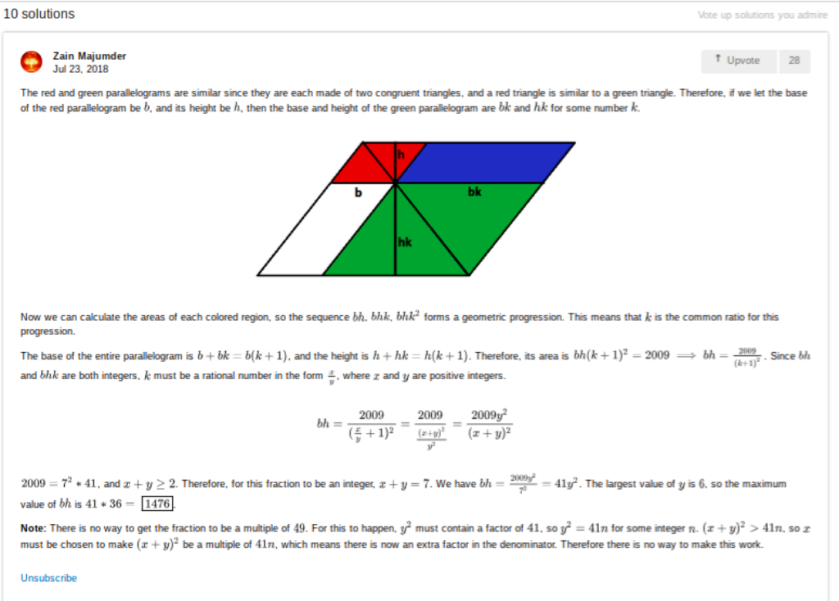
My beef is with that diagram. The answer given works on the red section being the largest part of the parallelogram whereas the diagram shows it as the smallest, which was the basis on which I worked. This is way beyond a diagram being “not to scale”, which I have no great issue (the most famous of all such schematic diagrams, variations of which can now be seen representing transport systems in cities everywhere in the world is of course H C Beck’s London Underground diagram), but showing what is actually the lagrest single area of the diagram as the smallest is a bridge too far (Beck enlarged the central area so the stations were easier to see, but he did not actually make it cover a larger area than the surrounding suburbs, merely a less small area than was actaully the case, which to me is what if the approach is to have any validity is what “not to scale” should mean). The diagram in this question was literally worse than useless – wkith no diagram at all it would be have been a better question than it was with the actual diagram.

ANSWERS TO THE TWO FABULOUS PROBLEMS

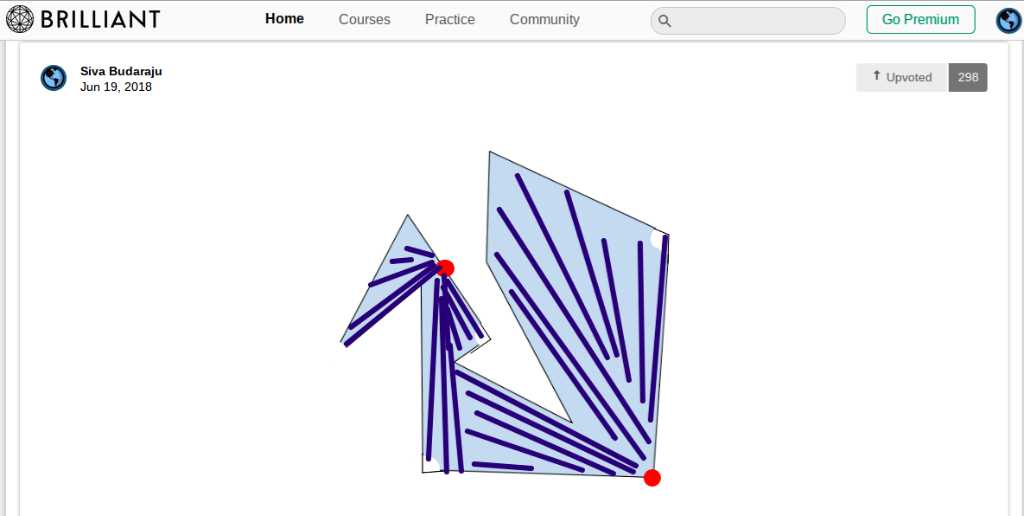
First, what I now call the “Mendrin Circles Problem” after its creator:

Here is Albert Lau’s published solution:

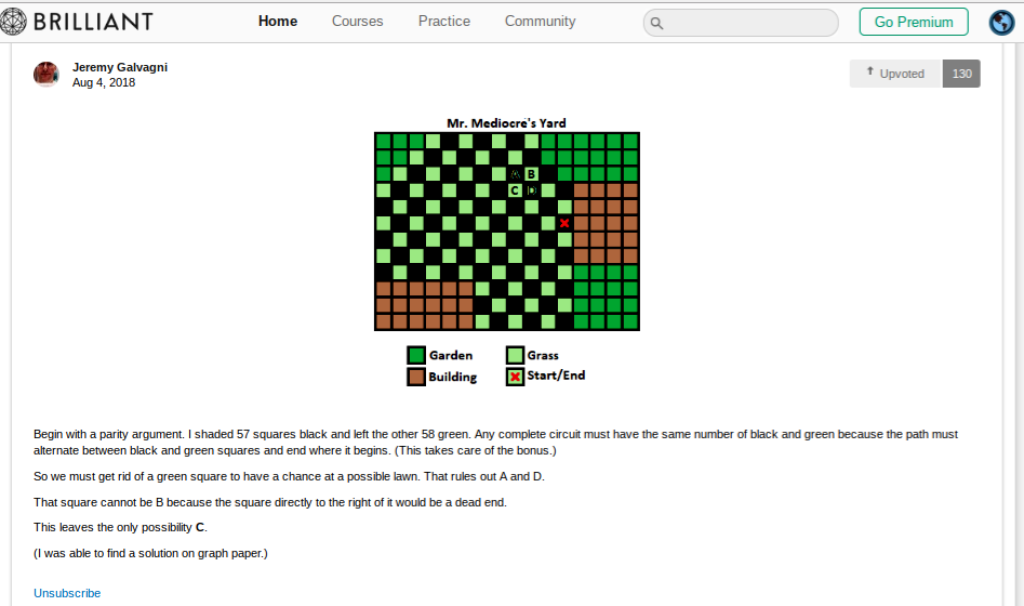
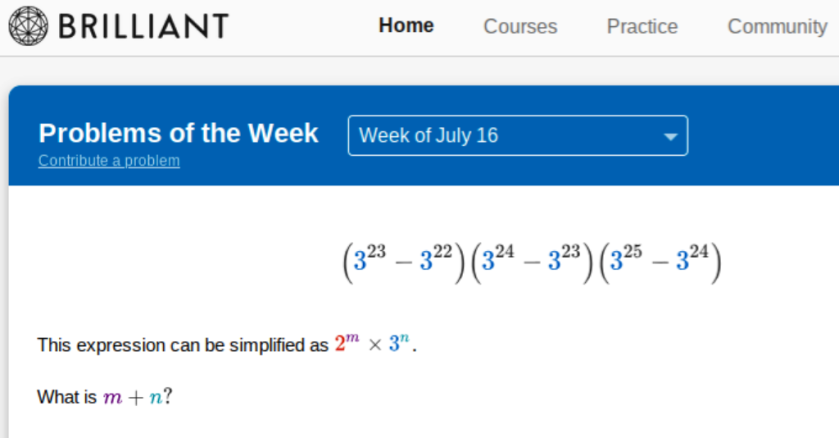
Second, the problem of Mr Mediocre’s Lawn:

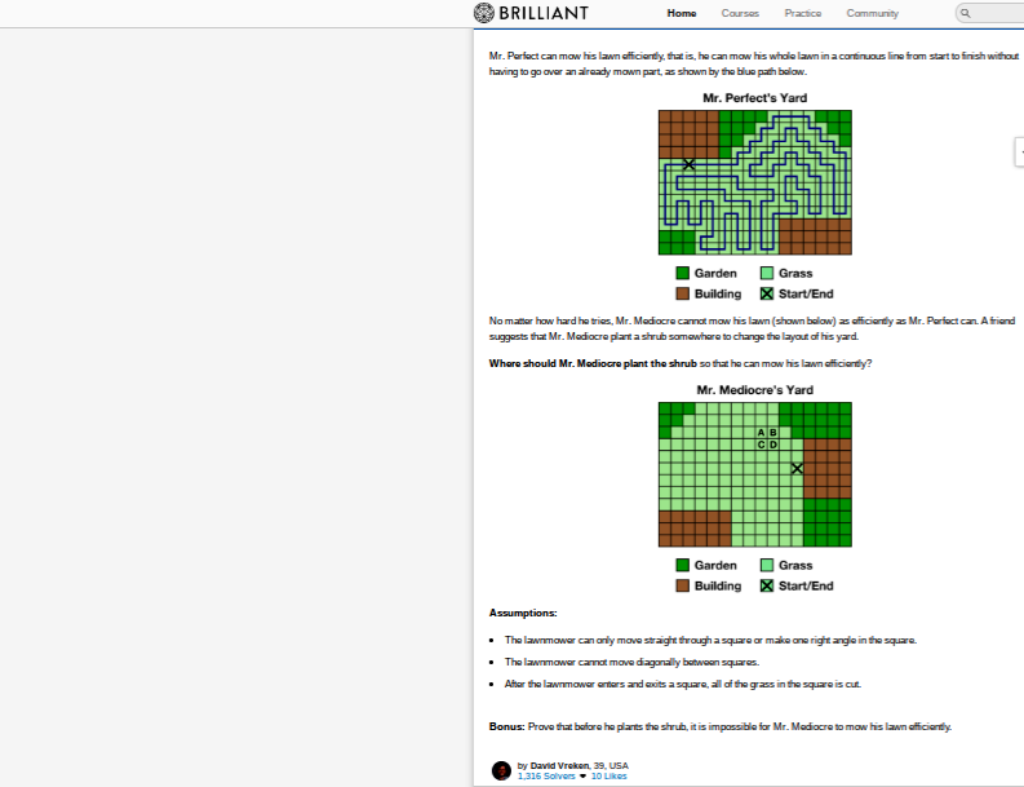
First the answer:

Jeremy Galvagni’s published solution was worthy of this splendid problem:

The ‘chessboard shading’ in this diagram is the key to the excellence of this solution – it rules out A and D, while B’s location rules it out, leaving only C as an option.

THE BONUS PROBLEM

The answer:

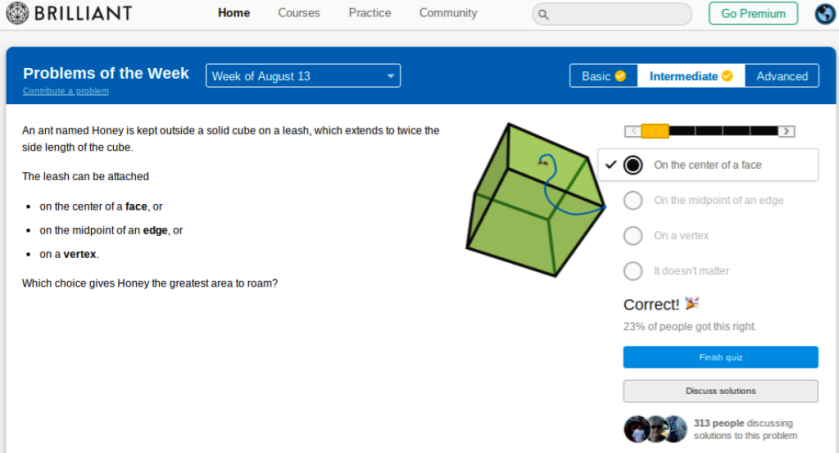
Attaching the leash to an edge or a corner introduces restrictions which are not there if it is attached to the centre of a face. At full extent Honey can be diametrically opposite her starting position, which means that the entire surface of the cube is available to her.

A NEW PROBLEM

This is a very old problem indeed:

Solutions to Guards and Clock Problem

Solutions to na couple of problems and a new problem for you to get your teeth into.

INTRODUCTION

A couple of aeons ago in the post I put up immediately before setting off for Marxism 2018 I presented two problems from brilliant.org, one easy and one hard. Now at long last I offer solutions to them.

THE GUARDS PROBLEM

Here is the answer:

Now here is an official solution, posted by Siva Budaraju:

Yes, Anna, you were right about this one, as you are about many things.

THE CLOCK PROBLEM

For this one I shall present the confirmation that my answer was correct, my sneaky way of solving the problem and then an official solution.

I got the solution by realising that if there was an arrangement of the hands that enabled this to happen it would not be unique – as with problems involving two hands on a clockface there would be a number of possibilities, which would mean that finding such an arrangement would not be very difficult, and this was supposed to be a dificult problem, which led me to the conclusion that there could not be a time when the three hands divided the clockface into equal segments. Now here are two official solutions:

A NEW PROBLEM

I finish by sharing another problem with you that I enjoyed solving:

Solutions (And New Problems)

Solutions to my .last set of problems and a new set. Also some photographs.

INTRODUCTION

It has been a few days since my last post, and the principal reason for this will made clear in my next post. Meantime I am starting proceedings for today by answering the questions I included in my previous post, and then setting a couple of new ones.

SOLUTION 1 – TRIANGLE CENTERS

Here is the original problem, from brilliant:

Here is the answer:

To explain, here is Alex Warneke’s published solution (one of a number, but the one I like best)

Draw a circle around each figure. The circle drawn around each polygon has a larger circumference than the polygon and therefore a larger radius than the circle. If we consider the ratio of circumference of a circle to perimeter of inscribed regular n-gon we see it is bigger for smaller n and smallest for n = 3.

SOLUTION 2: EBBINGHAUS DISILLUSION

This was the problem:

The two blue circles are exactly the same size. Here is an edited version of the above, deliberately clumsy so that my method of editing it can be seen by all:

PROBLEM 1: DECK OF CARDS

The first of two new problems from brilliant that I am sharing in this post:

This is a multi-choice question, the possible answers being:

a) Less than 50%
b) More than 50%
c) Exactly 50%

PROBLEM 2: GROYNE

Again from brilliant:

As the title of this section indicates I have identified a clear-cut mistake in the wording of the question – there may be room for doubt as to whether the indicated structure is a groyne or a jetty, but it is most definitely not a ‘breakwater’ – such would be entirely out at sea, not stretching from the land into the sea.

PHOTOGRAPHS

What is Autism?

Some thoughts about autism provoked in a good way by anonymouslyautistic and a bad way by the folk at magiquiz.

INTRODUCTION

I am not going to attempt a scientific answer to the question in my title, merely to lay out some of my own thoughts. The original inspiration for this post was a post produced by anonymouslyautistic, titled “WHAT IS AUTISM – FROM AN AUTISTIC’S PERSPECTIVE” and brought to my attention by americanbadassactivists. As readers of this blog will be aware I am branch secretary of the National Autistic Society’s West Norfolk branch as well as being autistic.

WHAT AUTISM IS NOT

Among the things that autism is sometimes supposed to be but is not are:

A form of mental illness (more on this at the end of this section as you will see).
A disorder
Something to be feared or worse still hated
Something that needs to be cured

I end this section with an example that absolutely shocked me when I saw it by way of twitter this weekend. I invite readers of this post to collectively identify everything they can find that is wrong with the formulation of the question below:

If you click on the image you can go to the quiz, take it yourself and then post a comment (if you choose to do this please follow me in highlighting the problems with this question).

AUTISM AND ME

My unsuitability for front-line customer service and the difficulties I have with communication are down to autism. On the other side of the ledger my eye for detail, reflected in my photography among other things, my mathematical skills, my aptitude for working with computers and several other of my strongest attributes are also due to autism.

I will finish this section by reminding people that different does not necessarily mean less, and that we are autistic people – note the emphasis given to the second part of that designation.

PUZZLES

In this section I provide the solution to one puzzle and offer another for your inspection. Both are mathematical in nature.

In ‘Midweek Mixture‘ I set the following puzzle:

The above table shows two putative sets of coin toss records, each for one coin tossed thirty times. Which is more like to be genuine based on what you can see?

a) series one
b) series two

To begin the solution, here is the table above with a column added:

You will see that the two sets of coin toss lists in the original problem were made up, but if you look at the results for the set of coin tosses I actually performed you will note that it looks much more like series two than series one – randomness is clumpier than we intuitively expect (the idea for this problem came from a book by Natalie Angier, in which she tells the story of a teacher who uses an experiment in which half of her class are assigned the task of inventing a series of coin tosses, and half of actually tossing coins and recording the result, while the teacher goes out of the room – and nearly always the teacher can tell the real from the fake).

My new problem comes from the mathematical website brilliant:

PHOTOGRAPHS

As usual I end this post with some photographs, in this case featuring a family of swans I saw swimming along the Gaywood River yesterdary morning:

	Thomas on 49
	Shaun Bradford on 49
	Thomas on Reaching Back to WG Grace Twic…
	Elena Delle Selve on Reaching Back to WG Grace Twic…
	Thomas on Two Contrasting Routes to…