England Selectors’ Ostrich Impression and Other Stuff

Some thoughts on the (in)action of the England selectors this week, some mathematical teasers and a few pictures.

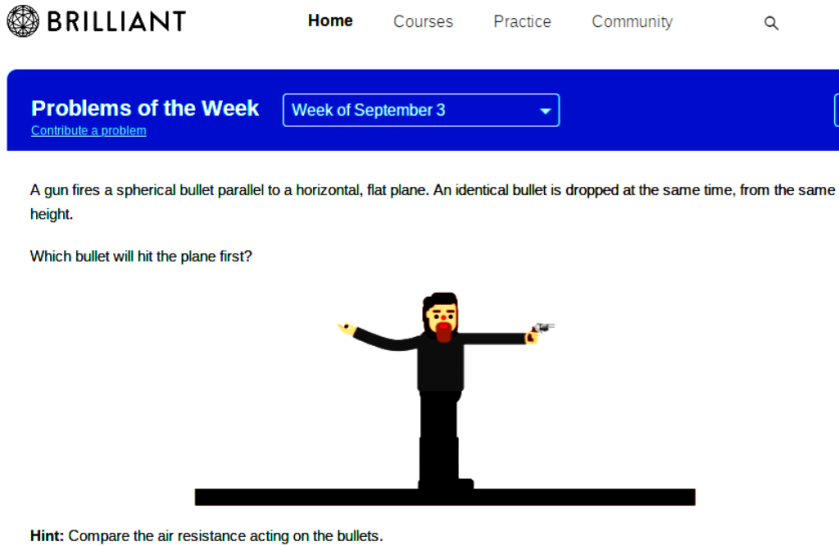
INTRODUCTION

A couple of days ago I wrote about England’s series win over India and presented some problems and solutions. This post is on similar lines, dealing with the actual behaviour of the England selectors and my thoughts thereon.

AN OPPORTUNITY SQUANDERED

England, with the series already in the bag, had a diamond-encrusted golden opportunity to experiment with options to fill gaping holes in their top order. Cook’s announcement of his impending retirement from international cricket should have acted as an extra spur. Instead of which we see very little in the way of forward planning or of experimentation of any sort. Even with the certain knowledge that a new opener will have to come in to replace Cook the selectors persevere with the proven failure Jennings.

Three individuals who can feel more aggrieved than most by this behaviour are Rory Burns (another 90 against Essex yesterday after the latter won the toss and chose to bowl first), Dan Lawrence and Liam Livingstone.

In view of Cook’s impending retirement I would have recognized openers at 1,2 and 3 (not a bad approach in test cricket anyway), with a view to the two other openers than forming a partnership in future matches. This is why in the previous post I mentioned Tammy Beaumont, a recognized opener who has been scoring stacks of runs recently. Batting is at least as much about timing and placement as it is about brute power, and that is why I believe (unlike in the case of fast bowling) a woman could mix it with the men even at the highest level, similarly with slow bowling and possibly wicket-keeping (for my money the best user of the gauntlets in world cricket across the board at the moment is Sarah Taylor). A number of the all-time greats of test match batting have been of diminutive stature (Bradman, Gavaskar, Tendulkar, Sehwag, Hanif Mohammad and several of the finest Sri Lankans spring to mind instantly). I am well aware that this super-radical option will not happen, but the alternatives that that leaves with are:

Two brand new openers, neither of whom have any experience of international cricket.
One new opener and one opener who has shown already that they are not actually good enough (Jennings)
Two openers who gave failed to prove themselves (presumably Jennings and a recalled Stoneman).

Of those three options, none of which massively appeal, my choice would number 1, which might end up working out well, and then the question is who to choose to open alongside Burns (whose case for selection is undisputable in the circumstances).

Having taken the “ostrich option” re their top order difficulties the only outcome from this game that could be acceptable is not merely a win to make it 4-1 for the series but a win by a massive margin. The timidity of the England selectors means that at least one and possibly two England openers will be starting their careers on overseas tours, with their first home test series being against those well known softies, the Aussies.

PROBLEMS AND SOLUTIONS

I will start as usual with answers and solutions to the previous problems (all from brilliant.org) before offering up some new problems.

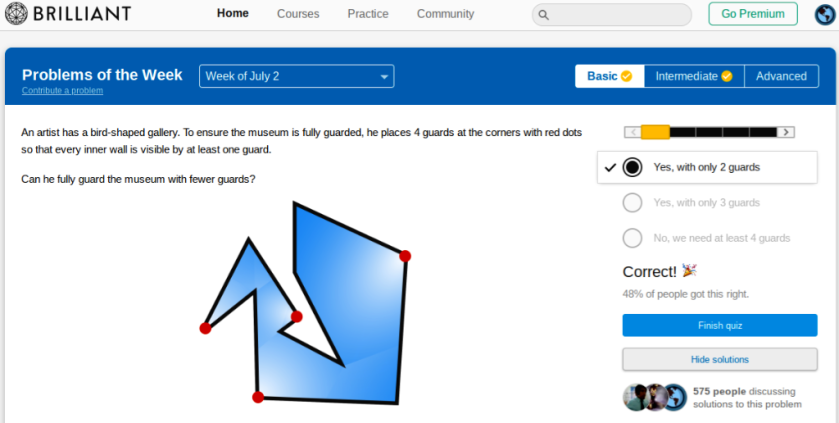
WHAT IS THE AREA OF THE QUADRILATERAL

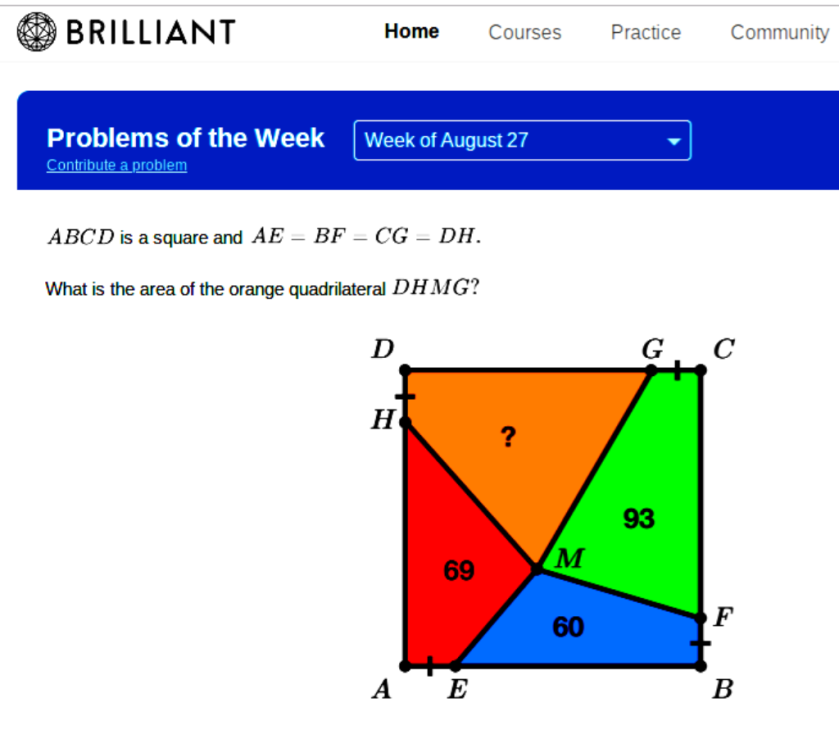
First the answer:

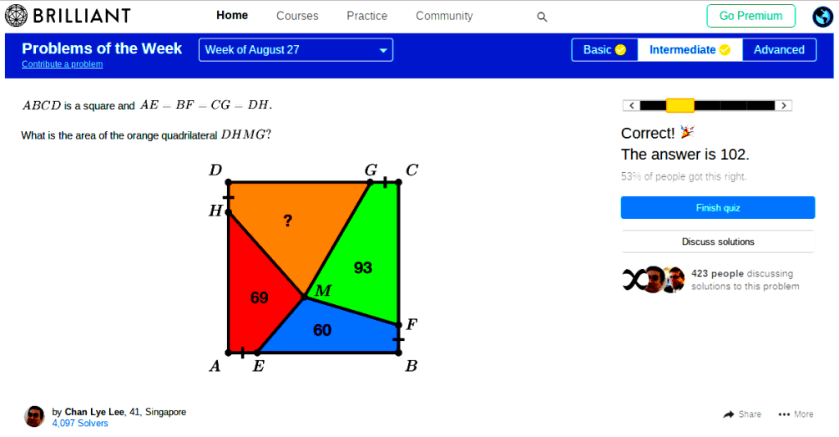
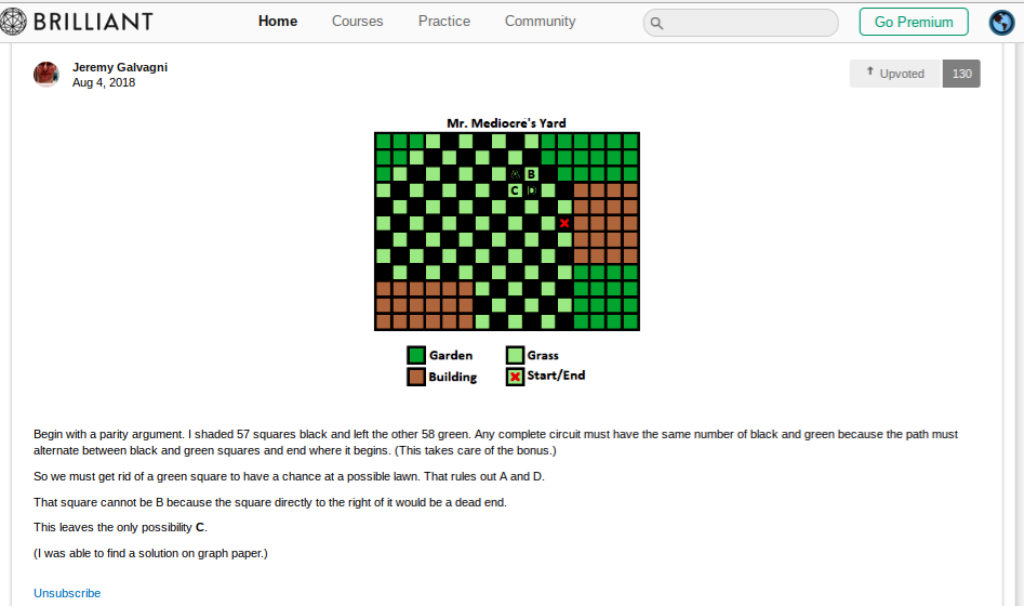
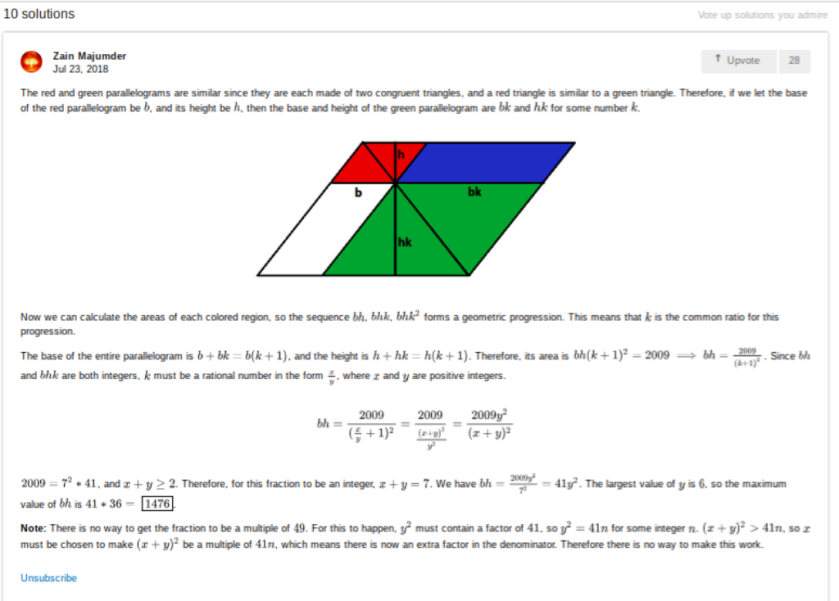
The hackers solution is that there are only two really serious possibilites since the shape is a square, namely 67 (giving an area of 289 = sides 17 units long) and 102 (giving an area of 324 = sides 18 units long), and since the question gave one three tries just enter those values for the first two tries (if your first entry does not come up right). Here, courtesy of Jeremy Galvagni is an elegant genuine solution:

THE .99 STORE

First the answer:

The figure in front of the .99 part of the price can vary, so all we need to know is how many .99s add up to answer ending in .89, and the answer is 11 (11 x 99 = 1,089, so 11 x 0.99 = 10.89), and the next number of items after 11 that would give us an answer ending in .89 is 111, the lowest price total for which would be $109.89. Thus Marie purchased 11 items.

NEW PROBLEMS

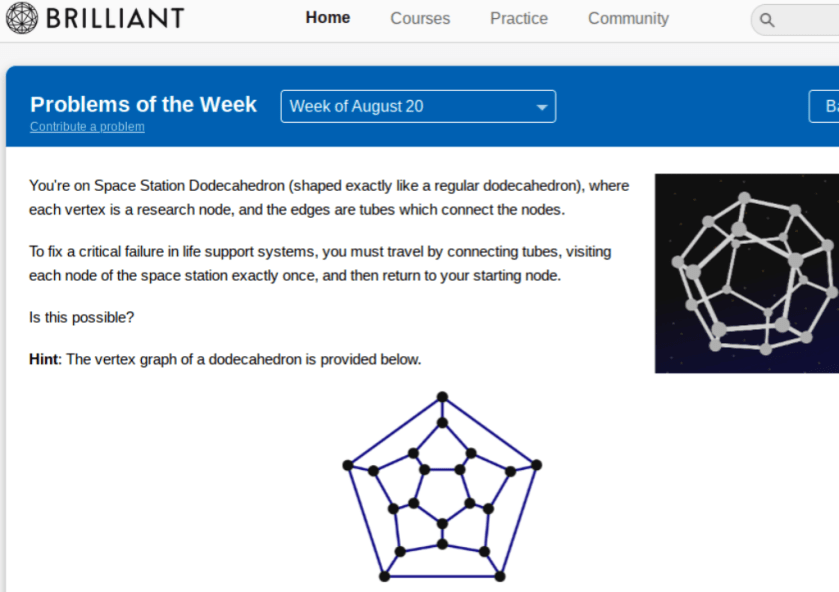
First an astronomy themed problem:

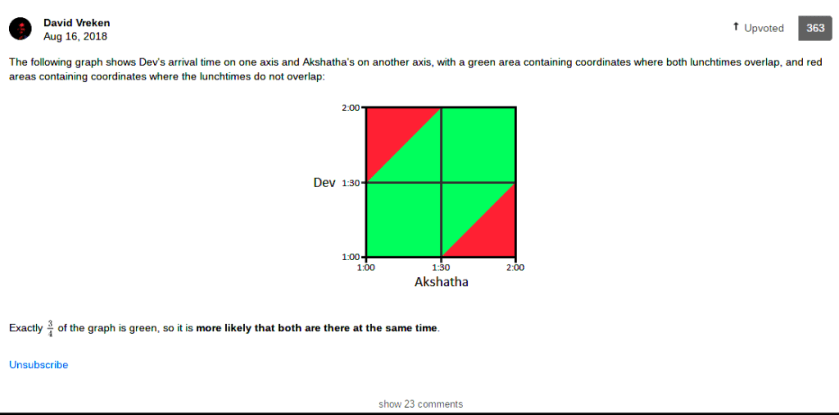
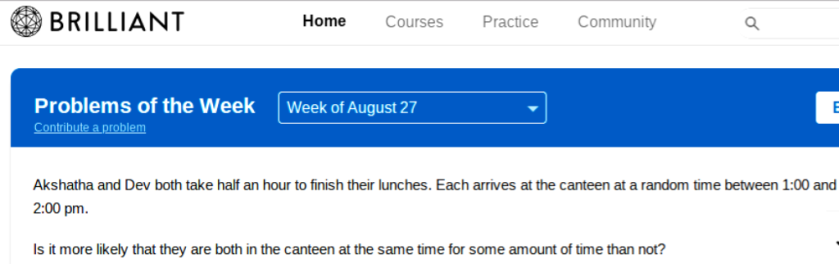
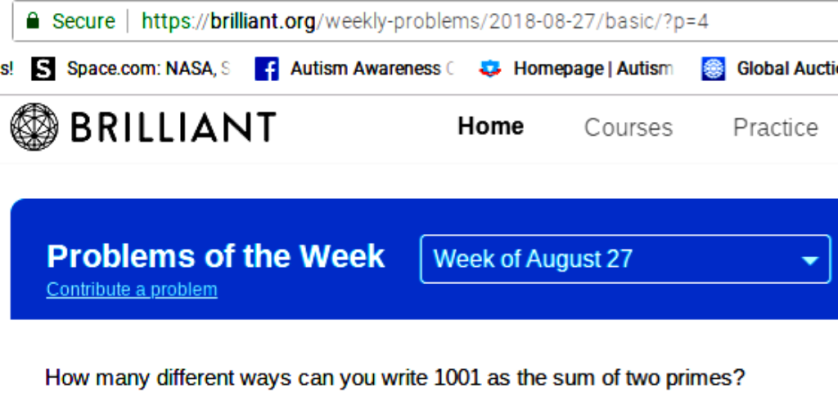
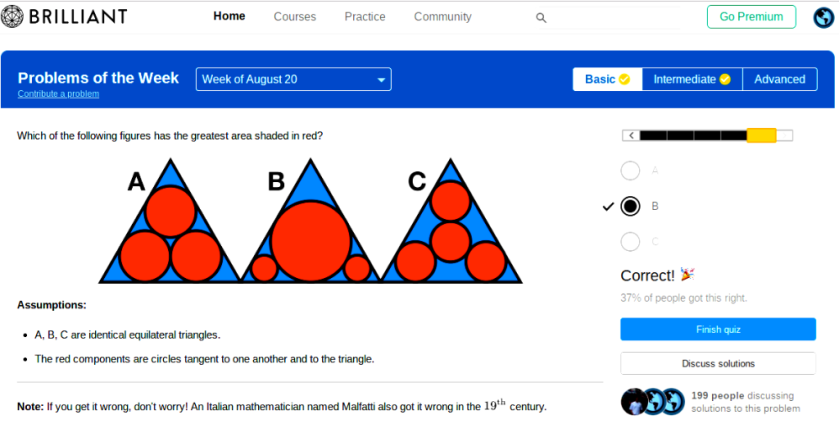
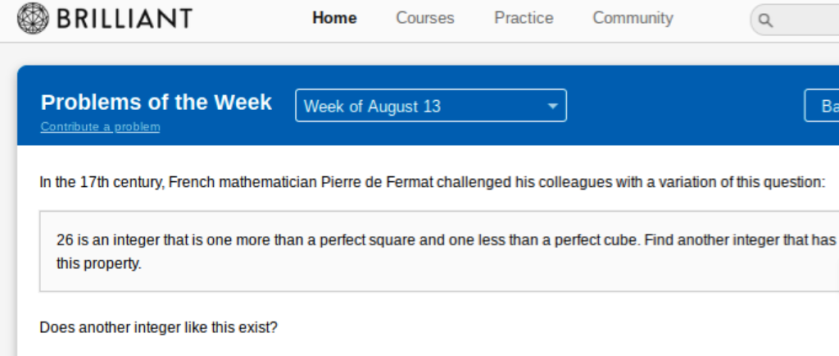
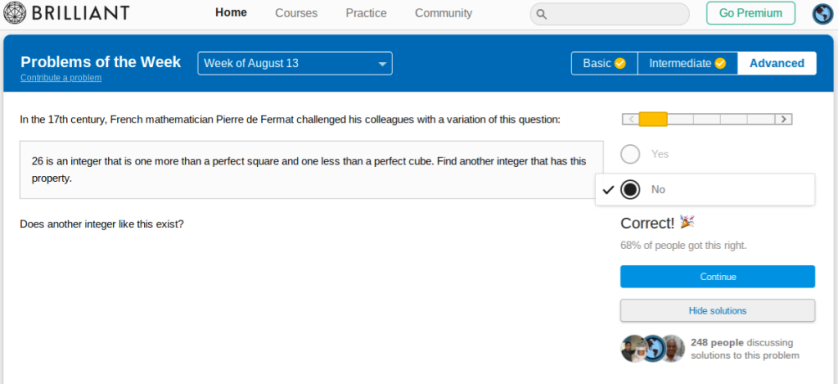
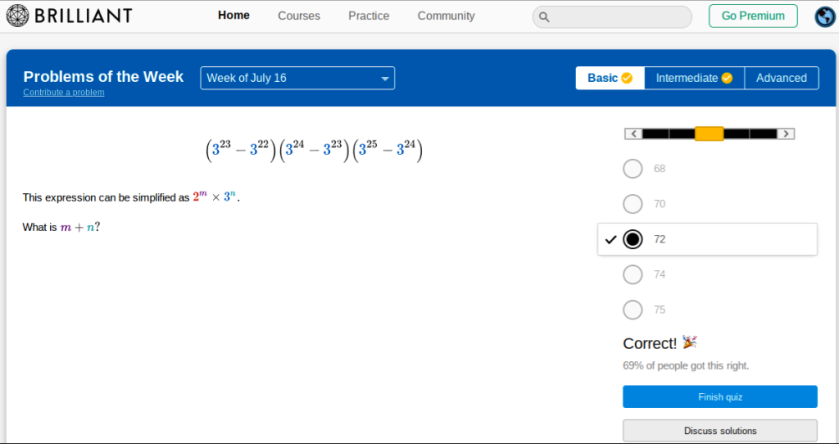
Now a question that has got almost three-quarters of those who tackled in on brilliant, but is not actually difficult:

PHOTOGRAPHS

Congratulations to England on a Series Win Against the World Number One Ranked Test Nation

Congratulations to England on their series win, a farewell to Alastair Cook who has announced his impending retirement from international cricket, some maths problems and solutions and some photographs.

INTRODUCTION

This is going to be a long post because there is a massive story to cover concerning the cricket in addition to the match itself. I will also be including some mathematical problems and solutions and of course some of my own photographs.

ENGLAND WIN A THRILLER TO TAKE THE SERIES 3-1 WITH A MATCH TO GO

On Thursday when England stumbled to 86-6 after winning the toss and batting I was not expecting to be writing a piece of this nature. England failed to polish off the Indian first innings when they had a chance of a lead. When Stokes stuffed skipper Root (run out 48) it was 122-5 and England led by only 97. Then came another lower order fightback, and with Curran adding 46 to his first innings 78 England set India 245 to win. The match was settled while I was at the Mencap Beach Hut, Old Hunstanton on an NAS West Norfolk day out. As usual the key wicket was that of Kohli, and once he had gone India never got back into contention, Moeen Ali adding four wickets to the five he took in the first dig (he is very much a bowler who likes being at home – 91 wickets at 31 in England, 51 at 52 abroad) to help settle things. In neither innings did England’s top order deliver sufficiently (a recurring problem). Aside from Root’s 48 from his preferred no 4 slot in the second innings, the highest score from an England player in the top four was Jennings’ second innings 36. I am now going to through England player by player.

A N Cook – see next section
K K Jennings – a failure in the first innings, and in many ways a worse story in the second – an opener who gets as far as 36 should be settled in for the long haul. I believe that with the series safely won and the situation ripe for experimentation he should be dropped.
J E Root – the skipper dropped himself to no 4 in the second innings and it took a run out to get rid of him then.
J M Bairstow – he was sufficiently injured to prevent him from keeping but not apparently from batting, but if he is to play as a specialist batsman it should be at no 3.
B A Stokes – the new, responsible Stokes played well up to a point in this match but in the second innings he overdid the blocking to the point of handing the initiative to India. Also running out the skipper never looks great (save perhaps at Christchurch in 1978 when Botham, allegedly acting on instructions from vice captain Willis to do whatever was needed to up the run rate, stitched up skipper Boycott).
J C Buttler – one of only two England batsmen to have topped the 250 run mark thus far in the series (the other being the wunderkind Curran) and competent behind the stumps.
M M Ali – a useful batting effort after England’s disastrous start on day 1 and two good bowling performances. His mid-match promotion to number three (where he did recently hid a double century for Worcestershire v Yorkshire) shows how desperate England are to find a way for Root to bat at four.
S M Curran – about the only thing the youngster hasn’t done in this series is walk on water! He is establishing himself as a star player.
A U Rashid – a poor match with both bat and ball, but he is too good not be firing again soon.
S C J Broad – a solid match for the veteran new ball bowler. He has now drawn level with Sir Richard Hadlee in the all-time test wicket takers list.
J M Anderson – a quiet match for one of the all-time great swing bowlers, but even though he did not take many wickets he continued to command respect.

I will end the cricket part of this post by naming my team for The Oval.

FAREWELL ALASTAIR COOK

Alastair Cook, after 160 test matches, the last 158 in sequence (the longest unbroken run of appearances in test history, and not likely to be challenged any time soon) has announced that the last match of this series, at The Oval, will be his international swansong. This marks the end of an epoch not just for England but for test cricket – in many ways Cook is the last true test match batsman, having made his debut before T20 was a really major thing and unlike many who get seduced by the bright lights and big money at tournaments such as the IPL he abandoned short form cricket to concentrate on his test match career. His achievements in test cricket placve him firmly among the greats of the game, and I think he has timed his announcement exactly right, bowing out on his own terms (which he had more than earned the right to do) and before too many people began to ask just why he continued to be picked.

On the 2010-11 Ashes tour Alastair Cook had to most successful visit to that part of the world by anyone named Cook since Captain James called by in 1770, and the most successful by an England batsman since Hammond in 1928-9. He played three monumental innings in that series, a match saving 235 not out at the Gabba (also sometimes referred to as the ‘Gabbatoir’ on account of what often happens to visiting sides there), his 148 at Adelaide that set the stage for the Pietersen innings that put Australia right out of that game and the 189 at Sydney in the final game that ensured that the final scoreline for the series would reflect England’s dominance (a 2-2 draw would have been an utter travesty, and even 2-1 to England after a drawn final match would have looked better than Australia deserved).

I have no doubt that there will be occasions in the near future when England find themselves wishing for Cook’s cool head and fighting qualities. It will be hard to get used to an England order without the name Cook at the top of it.

From this huge cricket fan and devotee of test cricket the message is “Well done Alastair, and thanks for some fabulous memories, especially of the Aussies being humbled in their own backyards”.

THE TEAM FOR THE OVAL

HI do not expect that thsi team will actually be picked (!) but it is what I would do in these circumstances, with the series already won: A N Cook, R J Burns, T T Beaumont, *J E Root, O J D Pope, S M Curran, +J C Buttler, M M Ali, A U Rashid, S C J Broad, J M Anderson.

PROBLEMS AND SOLUTIONS

I begin with the solutions to the two problems I posed in my last post:

AKSHATHA AND DEV

I give you a beautiful published solution from David Vreken:

1001 PROBLEM

Here is the answer:

I published a solution to this problem, which although more than half of all solvers got it wrong is actually very easy. My solution:

1001 is odd, and the only even prime number is two.
1001 – 2 = 999, which is obviously divisible by three (full prime factorization is 3 x 3 x 3 x 37)
Negative numbers do not apply to these questions as with them no number matches the definition of a prime, but even if they did, 1,003 (1,001 – -2) is composite anyway (17 x 59).

WHAT IS THE AREA OF THE QUADRILATERAL?

This is first of two new problems from brilliant.org for you:

There are two ways to solve this one, the official method and a hack (no bonus points awarded for guessing which method I adopted!).

HOW MANY ITEMS?

Incidentally this question should not be taken as suggesting that I approve of this method of pricing – the reverse is actually the case, I think it is utterly ridiculous and very irritating.

PHOTOGRAPHS

Church, North Norfolk — A church in North Norfolk

The new ‘Sandcruiser’ wheelchair at the beach hut.

Sandcruiser in action — The sandcruiser in action

Dolphin kite — No – not a real dolphin performing a record breaking acrobatic feat – merely a flashy kite being flown in the breeze.

Bentley I — A vintage Bentley (six shots in total)

Amber — Possibly a small piece of amber with something preserved inside it.

Cricket and Other Stuff

Cricket, in the course of which I make a very radical suggestion for dealing with England’s top order woes, and a few other things, including Maths and Public TGransport.

INTRODUCTION

As well as some stuff about the state of play in the current England vs India series I have a couple of mathematical problems for you and some of my own photographs at the end.

ENGLAND’S DREADFUL START

England won the toss yesterday morning before the fourth test match of the five match series against India at the Ageas Bowl, ~~Botley~~ Southampton. This was the last thing they managed to do right for some considerable time. At last, with the scoreboard reading a barely credible 86-6, Sam Curran, inexplicably dropped from the last test match and now returning to the fray, emerged from the pavilion. Much of the carnage was more due to good Indian bowling than bad batting, although Jennings (already on borrowed time for my money) will not want to see replays of his LBW (however good a piece of bowling it may have been padding up to one which would have uprooted the middle stump otherwise never looks good). Fortunately England’s tail managed to produce a diplodocid (see picture at end of this paragraph) proportion of the innings. Curran, making the ridiculous decision to drop him from the previous game look positively ludicrous, racked up 78 before he was last out, the total hvaing reached a semi-respectable 246.

Diplodocus — This is why I described the contribution of the England tail as being of diplodocid proportions.

India are currently 135-2 in response. Only once in test match history has a side come back from 0-2 down to take a five match series, in 1936-7 when Australia’s comeback was fuelled by scores of 270, 212 and 169 from Don Bradman in the course of those last three matches. In 1894-5 Australia levelled the series at 2-2 after being 0-2 down but Andrew Stoddart’s England rallied to win the decider.

England’s continuing top-order woes need to be addressed if they are to avoid surrendering a series on which they seemed nto so long ago to have a vice-like grip. Rory Burns must come into the side in place of Jennings. I would also bring Pope back but place him lower in the order. brief interjection – BIG NEWS – Kohli Is Out! Also, thinking about the need for top order runs I now tender a suggestion far more radical than Rory Burns – there is one England opener who has making stacks of runs all over the place of late – the one and only Tammy Beaumont! The way they have performed thus far none of the current top order are entitled to object to that suggestion.

Yes going with two new openers would be a colossal gamble, but they could scarcely fare much worse than Cook and Jennings have in this series.

A COUPLE OF MATHEMATICAL TEASERS

Both of these, from my usual source, are very easy problems which have tripped a number of solvers up. I give them in the reverse order to which they appeared:

And

HERITAGE OPEN DAY

Heritage Open Day this year is Sunday September 16th. There will be some 60 sites open in the King’s Lynn area, and if you there on the day do make sure you visit. If you happen to visit the cellars at the Bank House between 12 noon and 2PM I will be one of the volunteers you encounter.

TWO STORIES OF BRITISH PUBLIC TRANSPORT DAFTNESS

I start this section with the more minor but also more personal of these stories. Today I made my travel arrangements to Sheffield for a cousin’s wedding. I checked bookings from King’s Lynn to Sheffield, and the cheapest ticket would have cost me £68.20. Knowing that a ‘plan B’ was available I then checked out bookings from Peterborough to Sheffield and lo and behold up came a ticket for just £38.50, which when the two bus tickets on the ExCel are added in amounts to £51 all up. In other words to have travelled by train from King’s Lynn all the way to Sheffield would have cost me 33% more than the combined bus/ train route I am actually taking. Now of course not everyone booking this journey would have known of the alternative, and I wonder how many people have been swindled in this.

My second story of public transport daftness is that The Elizabeth Line (aka Crossrail) will not now be coming into service until nearly a whole year later than planned (more here).

PHOTOGRAPHS

The pictures here are of items I purchased at our auction on Wednesday (it was reasonably successful, with a few big sales, and a lot of items finding buyers).

Lot 121 – I scanned these items rather than photographing of them.

Under a viaduct and over a bridge — A photograph of the item taken this morning

360 — Two of the four items in this lot were of sufficient interest for me to consider bidding, the Nobel Prize cover, and the one that really settled it, the Classic Locomotives.

Classic Locomotives FDC — The main cover photographed this morning.

Classic Lcomotives stamps II — The first of two close-ups of the stamps (the reflectivity of the protective covering makes this a challenge).

Classic Locomotives other side — The ‘cover’ part of this item contains a lot of information when opened up (see also next picture for the other side).

A Mixed Bag for Monday

Solutions to my last two maths problems, some sciencey pieces, a petition and some photographs.

INTRODUCTION

This post includes solutions to the problems I posed on Saturday, and a few other things from various sources.

SPACE STATION DODECAHEDRON

Here is the question as a reminder:

Here is the answer:

Here is a splendidly concise solution from David Vreken:

A VARIARION ON THE MALFATTI THEME

Here is the question:

Here is the answer:

In the 19th century Malfatti conjectured that the way to maximise the area of a triangle you could fill with three circles was to fill in the three largest circles that touch specifically two of the three sides. Although he was not alive to be humiliated it turned out that he was not merely wrong, his proposed solution has been proved not to work for a single triangle. The solution that always works is first put in the largest single circle that touches all three sides that you can, then fill in the largest circle you can in the remaining space and then do so again. In an equilateral triangle the difference is small, but in a long thin isosceles triangle it is quite substantial.

Here is Jeremy Galvagni’s published solution:

SCHOOL REFUSAL SYNDROME PETITION

This on the official site for petitions to the UK government, which means that you have be a UK citizen to sign it. Please click the screenshot below to sign and share it if so minded:

A TRIO OF SCIENCE PIECES

First a fascinating piece from the National Geographic titled “Can Today’s Whale Species Survive the age of Humans” which covers the past and present of the cetaceans and speculates about their future.

David Quammen, a good writer and a useful scientist to know about if you are planning an A to Z post, has a new book out on the subject of evolution, and Jerry Coyne of whyevolutionistrue has provided a very detailed review of it.

Finally, a letter to the Guardian signed by 60 well known environmental campaigners declaring their unwillingness to debate with climate change deniers, and why they are unwilling to do so. Below is the opening to the letter (please click to visit the original) and a list of signatories:

SOME FINAL PHOTOGRAPHS

To finish here are some of my recent photographs:

A Solution and Some New Problems

A solution and a couple more problems from brilliant.org.

INTRODUCTION

On Wednesday I left you with a problem from brilliant.org to tacke having presented solutions to several others. Today I start with a solution and then present you with some new problems.

SOLUTION TO WEDNESDAYS PROBLEM

Here is the problem again:

Here is the answer:

And now here is Mark Hennings’ published solution:

As a side issue various commenters on brilliant.org demonstrated their failure to read the question by bringing up examples of numbers that are both square and cube (e.g 64), but these are utterly irrelevant since the question was about a number that is both one more than a square and one less than a cube.

NEW PROBLEMS

Two new problems for you, one easy, especially if you are familiar with the story of Signor Malfatti, and one slightly more difficult but quite fun.

CAN YOU OUTDO MALFATTI?

SPACE STATION DODECAHEDRON

Solutions to Good and Bad Mathematical Problems

Solutions to the problems I put up here on saturday and some new problems.

INTRODUCTION

On Saturday I produced a mixed bag of offerings from brilliant.org, promising to provide solutions in a later post, and now that time has arrived.

THE WORST SET PROBLEM I HAVE EVER ENCOUNTERED ON BRILLIANT

I got nowhere close to solving this for reasons which will soon become obvious.

Here is the official “correct” answer:

My beef is with that diagram. The answer given works on the red section being the largest part of the parallelogram whereas the diagram shows it as the smallest, which was the basis on which I worked. This is way beyond a diagram being “not to scale”, which I have no great issue (the most famous of all such schematic diagrams, variations of which can now be seen representing transport systems in cities everywhere in the world is of course H C Beck’s London Underground diagram), but showing what is actually the lagrest single area of the diagram as the smallest is a bridge too far (Beck enlarged the central area so the stations were easier to see, but he did not actually make it cover a larger area than the surrounding suburbs, merely a less small area than was actaully the case, which to me is what if the approach is to have any validity is what “not to scale” should mean). The diagram in this question was literally worse than useless – wkith no diagram at all it would be have been a better question than it was with the actual diagram.

ANSWERS TO THE TWO FABULOUS PROBLEMS

First, what I now call the “Mendrin Circles Problem” after its creator:

Here is Albert Lau’s published solution:

Second, the problem of Mr Mediocre’s Lawn:

First the answer:

Jeremy Galvagni’s published solution was worthy of this splendid problem:

The ‘chessboard shading’ in this diagram is the key to the excellence of this solution – it rules out A and D, while B’s location rules it out, leaving only C as an option.

THE BONUS PROBLEM

The answer:

Attaching the leash to an edge or a corner introduces restrictions which are not there if it is attached to the centre of a face. At full extent Honey can be diametrically opposite her starting position, which means that the entire surface of the cube is available to her.

A NEW PROBLEM

This is a very old problem indeed:

Good and Bad Mathematical Problems

Two splendid problems, one terrible one and one intermediate one, all courtesy of brilliant.org.

INTRODUCTION

This week on brilliant.org I have encountered two of the finest mathematical problems that I have seen on that site, and also unequivocally the worst. In the rest of this post I will share these problems with you – solutions and explanations will appear in a later post.

FIRST THE BAD NEWS

This is the terrible problem referred to in the introduction. In almost 15 months og being a brilliant.org solver I have complained about precisely one problem – this one:

The “correct” answer when I give it will make it clear precisely why I was so annoyed by the setting of this problem.

TWO FABULOUS PROBLEMS

These two problems were beautifully set, very fun to solve, and one has a published solution that I consider to be quite superb. First:~

I tackled this one this very morning:

A BONUS PROBLEM

Can you give Honey the ant maximum possible access to the surface of the cube?

Press Releases and Triangular Bridges

Some stuff about upcoming auctions and press coverage thereof and the solution to my most recent mathematical teaser.

INTRODUCTION

This post deals with some of my work at James and Sons and also includes a solution to a problem I posed last week.

PRESS RELEASES

In my recent post about James and Sons’ upcoming gold coin and proof set auction I included a copy of the official press release I had put out about it. What I did not mention in that post is that we also have a less significant ajuction coming up this Monday, for which I had also out out a press release. Both are reproduced below to set the scene for what follows:

On Thursday morning I checked into the James and Sons twitter account and was delighted to spot a link to an article in the Fakenham and Wells Times (part of the Archant stable and therefore connected to the Eastern Daily Press) about the coin auction. Below is a scan of the print version of this article:

Then yesterday morning brought more positive news – a link to an article in that day’s Lynn News about Monday’s general collector’s auction. The focus of this article is some documents we have relating to William Hoste, after whom The Hoste in Burnham Market is named, and who was a protege of Lord Nelson and connected by marriage to Robert Walpole. Here is a scan of the print version of this article:

We have another auction in preparation, and I have already pretty much decided that this 19th century presentation conductors baton (it is too large to have been intended to be used) will be the feature image in the press release for that one:

11-a — For me the local connection revealed here clinches it.

THE TRIANGULAR BRIDGES

Here is the problem I set last week, followed by the answer and an official solution:

Here is a concise solution, courtesy of Chew-Seong Cheong :

Walk for Wildlife

Advertising the Walk for Wildlife and attending to mathematical matters.

INTRODUCTION

The centrepiece of this post comes courtesy of the team4nature twitter account. I have also included the solution to a prnblem from brilliant.org and a new problem from the same source.

WALK FOR WILDLIFE

A SOLUTION AND A NEW PROBLEM

Here is the answer the problem I posed last week:

carrying out the subtractions in thte brackets above gives us (2 * 3^22)(2 * 3 ^23)(2 * 3^24). This becomes (2^3)(3^(22+23+24))= (2^3)(3^69). Thus m = 3 and n = 69, and 69 + 3 = 72.

As a supplement to this little problem, would you have an observation platform where the three bridge segments meet at the centre of the lake? This latter of course, unlike the mathematical question is purely a matter of opinion. I would go for a circular platform just below the level of the bridges, accessible by lifts and stairs.

Solutions to Guards and Clock Problem

Solutions to na couple of problems and a new problem for you to get your teeth into.

INTRODUCTION

A couple of aeons ago in the post I put up immediately before setting off for Marxism 2018 I presented two problems from brilliant.org, one easy and one hard. Now at long last I offer solutions to them.

THE GUARDS PROBLEM

Here is the answer:

Now here is an official solution, posted by Siva Budaraju:

Yes, Anna, you were right about this one, as you are about many things.

THE CLOCK PROBLEM

For this one I shall present the confirmation that my answer was correct, my sneaky way of solving the problem and then an official solution.

I got the solution by realising that if there was an arrangement of the hands that enabled this to happen it would not be unique – as with problems involving two hands on a clockface there would be a number of possibilities, which would mean that finding such an arrangement would not be very difficult, and this was supposed to be a dificult problem, which led me to the conclusion that there could not be a time when the three hands divided the clockface into equal segments. Now here are two official solutions:

A NEW PROBLEM

I finish by sharing another problem with you that I enjoyed solving:

	GP on A Cornish Christmas 1: A Curat…
	Renegades Blown Away… on England Fightback Comes Too…
	The First Two Days i… on A Successful Auction
	Marizanne’s Mastercl… on From Victory to Rout in Two…
	From Victory to Rout… on An Extraordinary Opening …